- 1 : le pouce pointe sur la première phalange de l'index,
- 2 : le pouce pointe sur la deuxième phalange de l'index,
- 3 : le pouce pointe sur la troisième phalange de l'index,
- 4 : le pouce pointe sur la première phalange du majeur,
Pourquoi compter ? Les chiffres sont particulièrement stimulants car ils les incitent à repousser les limites et à compter toujours plus loin. Et puis rien n'est plus gratifiant que l'activité de comptage tant les progrès sont visibles.
Pourquoi la base 60 ?
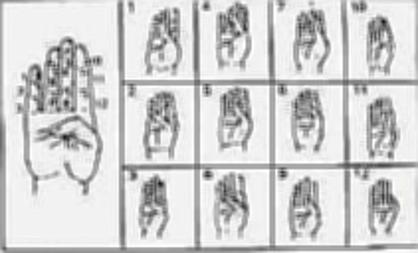
Les origines de la base 60 se cachent également sur nos mains : il s'agit d'une combinaison entre les 5 doigts de la main gauche et les phalanges des quatre doigts de la main droite, le pouce servant à compter les phalanges, soit 12 au total. Et 5 x 12 = 60 !
Comment se nomme les chiffres après la virgule ? Le premier chiffre après la virgule est le chiffre des dixièmes. Le deuxième chiffre après la virgule est celui des centièmes, et ainsi de suite jusqu'au dernier chiffre après la virgule.
Comment compter en octal ?
Le système de numérotation en octal est un système à base 8. Cela signifie qu'avec cette base on compte de 0 à 7, contrairement au décimal où l'ont compte de 0 à 9. Pourquoi on dit une douzaine ? Cette habitude remonte au… Moyen-Âge ! Et oui, à cette époque les commerçants utilisaient leur main pour compter et c'est naturellement le nombre 12 (comme le nombre de phalanges) qui a servi de base de calcul ; un nombre qui avait l'avantage d'être facilement divisible, par 6, 4, 3 et 2.
Comment s'appelle le bout des doigts ?
Les phalanges distales correspondent à l'extrémité des doigts.
Comment compter avec les mains ?
Qui a inventé les 24 heures ?
Historiquement, la division du jour en 24 heures remonte aux Sumériens. Il y a de 4000 à 5000 ans, ces habitants du proche-Orient divisaient déjà leur journée en six périodes : trois dans la journée, trois dans la nuit. Pourquoi 60 secondes et pas 100 ? Parce que cette base 60 était utilisée par les astronomes babyloniens pour leurs calculs, qui avaient remarqué que 60 est divisible par 2, 3, 4, 5 et 6, ce qui est bien pratique pour faire des quarts, des tiers.
