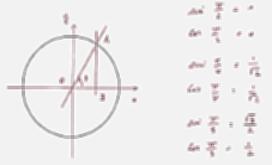
Quand θ est entre π et 3π/2, le sinus et le cosinus sont tous les deux négatifs. Et quand θ est dans le quatrième quadrant (en bas à droite) le cosinus est positif, et le sinus est négatif.
Quel est le signe de cos A ? Cosinus  = Côté adjacent (noté a) / Hypoténuse (noté h).
Comment réduire au premier quadrant ?
Exemple 1 Déterminer la valeur de sin240° . Comme 240° = 180° + 60° , nous allons obtenir la valeur de sin240° en utilisant un nombre trigonométrique de 60° . Le cercle trigonométrique ci-contre montre que 240° et 60° ont des sinus opposés. 4 , utilisons un nombre trigonométrique de π 4 .
Comment utiliser calculatrice scientifique iPhone ? Si vous souhaitez y accéder sur votre iPhone, il vous suffit d'ouvrir l'application Calculatrice, le moyen le plus rapide de le faire via le centre de contrôle auquel vous accédez en faisant simplement glisser votre doigt depuis le bas de l'écran.
Comment Calculer Arcos ?
Pour le calcul de l'arc cosinus d'un nombre, il suffit de saisir le nombre et d'y appliquer la fonction arccos. Ainsi, pour le calcul de l'arc cosinus du nombre suivant 0.4, il faut saisir arccos(0.4) ou directement 0.4, si le bouton arccos apparait déjà , le résultat 1.15927948073 est renvoyé.
Comment faire inversé cosinus ? La sécante de l'angle d'un triangle rectangle est l'inverse de son cosinus. Elle est égale au quotient de la longueur de l'hypoténuse par la longueur du côté adjacent.
Quelle est l'unité du cosinus ?
Le cosinus d'un angle ; dans un triangle rectangle ; est égal au rapport de la longueur du coté adjacent à l'angle sur la longueur de l'hypoténuse. qui n'a pas d'unité. Quel est la valeur du cos ?
| en degrés | 0° | 60° |
|---|---|---|
| en radians | π 3 | |
| cos | 1 | 1 2 |
| | 3 2 |
Quel est le cosinus de 120 degrés ?
D'où cos 120 = 1/2 ! Qui a inventé la tangente ? C'est la définition que l'on utilise aujourd'hui. C'est cependant Blaise Pascal qui, dans la première moitié du XVIIè siècle, a le premier mené des études sur la notion de tangente à une courbe ; lui-même les appelait « touchantes »...
