Quel est le logarithme de 2 ?

Ainsi, le logarithme binaire de 1 est 0, le logarithme binaire de 2 est 1, le logarithme binaire de 4 est 2, le logarithme binaire de 8 est 3.

Pourquoi utiliser les logarithmes ? Le logarithme est très couramment utilisé en Physique-Chimie, car il permet de manipuler et de considérer des nombres possédant des ordres de grandeur très différents, notamment grâce à l'emploi d'échelles logarithmiques.

Comment passer de log à ln ?

- log(N) = ln(N)/ln(10). -> C'est une formule de passage entre les différent logarithmes. Comment calculer le logarithme d'un nombre sans calculatrice ? Pour calculer à la main avec les log, on part de tables pré-existantes, et on utilise les différentes règles existantes pour les valeurs de non tabulées ; par exemple, pour calculer ⁡ , on utilise le fait que ⁡ ⁡ ( 2 × 3 ) = ln ⁡ ⁡ et les valeurs des tables ...

Quel graphique pour variable quantitative ?

VA discrète (quantitative discontinue) Ce type de variable est associée généralement à un diagramme en bâtons où l'axe horizontal des abscisses porte les valeurs prises par la VA (xi) tandis que l'axe vertical des ordonnées porte l'effectif absolu (ni) observé. Comment faire le log ? Si l'argument du logarithme est une multiplication de 2 facteurs, on obtient alors l'addition de 2 expressions logarithmiques. logc(M×N)=logcM+logcNRemarque : La valeur de la base ne change pas lorsqu'on utilise cette loi.

Pourquoi logarithme décimal ?

Le logarithme décimal ou log₁₀ est le logarithme de base dix. Il est défini en tous les réels strictement positifs x. Le logarithme décimal est la fonction continue qui transforme un produit en somme et qui vaut 1 en 10. pour x>0, si y = log₁₀(x) alors x=10^y.

Comment isoler un log ? Le but est en effet d'isoler dans un premier temps les logs. Pour cela, on fait passer tous les membres non logarithmiques de l'autre côté de l'équation. N'oubliez pas d'inverser les signes opératoires !

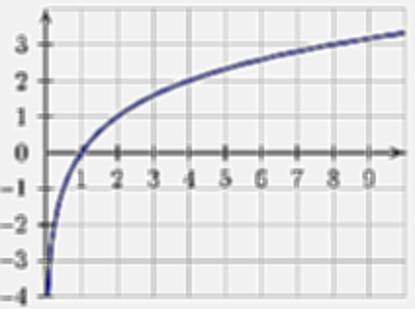
Est-ce que ln de 0 existe ?

Attention ! Beaucoup d'élèves disent ln() = 1, ce qui est archi-faux ! Par ailleurs, la fonction ln est STRICTEMENT CROISSANTE. On va également s'en servir par la suite. Quel est la limite de ln ? Les limites du logarithme népérien existent en 0 et +∞ (plus l'infini): La fonction logarithme népérien admet une limite en 0 qui est égale à -∞. La fonction logarithme népérien admet une limite en +∞ qui est égale à +∞.